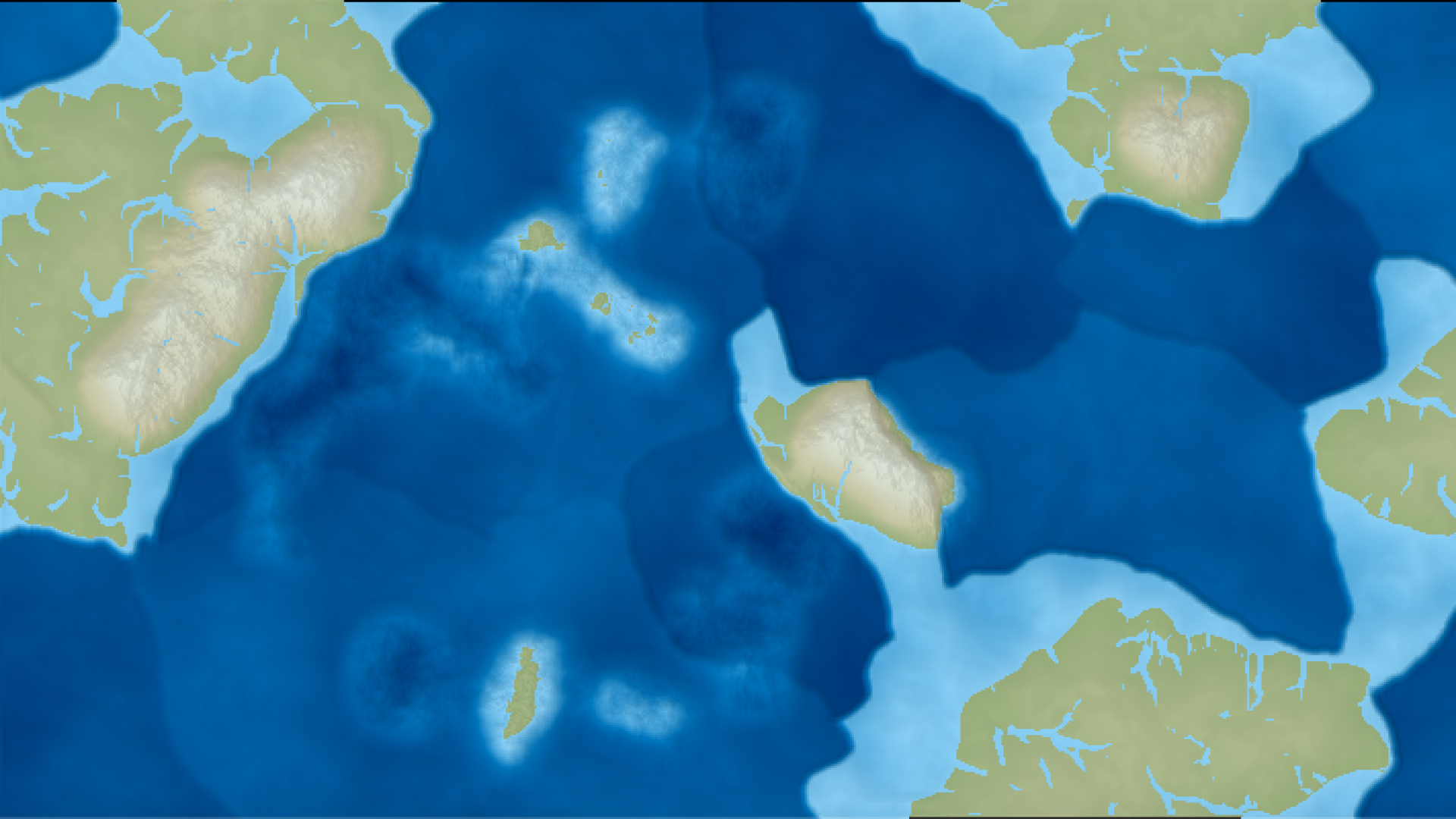
This isn’t a tutorial on Perlin/simplex noise. I just want to clarify some of the terms you may encounter in a noise library or on blogs discussing noise. If you are looking for a tutorial, check out adrian’s soapbox from whom I borrowed the images in this post or Google around for others.
Perlin and Simplex History
Perlin noise has an interesting history. The gist of it is that this guy named Ken Perlin was frustrated with the lack of natural-looking phenomena in computer graphics in the 1980’s so he developed an algorithm to generate natural-looking noise textures. He won some awards and the Perlin noise algorithm was used in everything from smoke to who knows what.
In 2001 he went back and created a similar but better (fewer visual artifacts and much faster, especially at higher dimensions) algorithm called simplex noise. Unfortunately, simplex noise didn’t replace Perlin noise for a few reasons.
First, Perlin noise was already “good enough” for many applications so there wasn’t much need for change.
Second, the nature of noise requires developers to spend a lot of time tweaking magic input numbers to obtain the perfect noise result. Switching algorithms requires finding many of those numbers all over again.
Third, implementing simplex noise requires some tricky math coordinate transformations.
Fourth, Perlin’s simplex algorithm is patented for certain applications, while the Perlin noise algorithm is not.
Because of the last point, if you want to use simplex noise (as it is better than Perlin noise), I recommend using the OpenSimplex algorithm, which isn’t patented. If you’re using a noise library, I similarly recommend making sure it’s using the OpenSimplex algorithm.
Gradient vs Fractal Noise
Technically, Perlin and simplex noise are gradient noises. That is, they create smooth, continuous functions without sudden jumps or sharp edges.
Fractal noise is noise that is similar when you zoom in or out. Technically, Perlin and simplex noise are only fractal noises when multiple different octaves are layered together with a consistent lacunarity and gain. However, you’ll pretty much always see Perlin/simplex noise with multiple octaves layered together so they’re generally considered fractal noises.
Hold Up: Lacunarity?
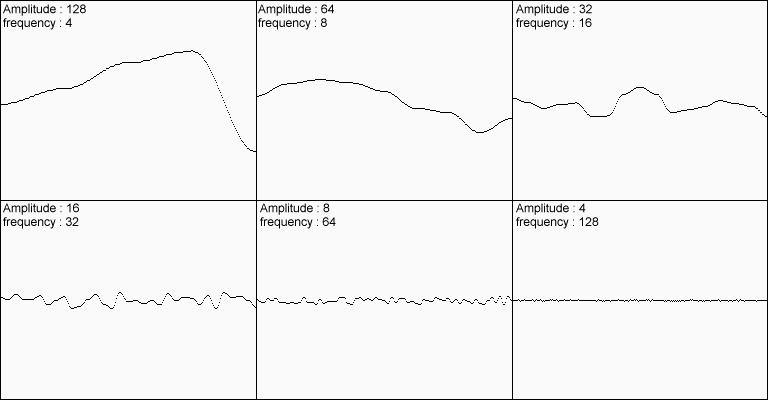
There are five main “settings” involved in Perlin/simplex noise (and these often apply to other fractal noises): amplitude, frequency, octaves, lacunarity, and gain.
Amplitude and Frequency
Amplitude is the height of a wave. Frequency is a measure of how many waves exist in a given interval. Frequency is the inverse of the wavelength, so sometimes you may see “wavelength” instead of “frequency.”

Octaves, Lacunarity, and Gain
Fractal versions of Perlin/simplex noise combine multiple octaves with varying amplitudes and frequencies (e.g. the six octaves shown above).
Lacunarity and gain measure how much the frequency and amplitude of each wave changes with each octave. For most applications, the lacunarity will be about 2 and the gain will be about 0.5, which means each octave will have twice the frequency (half the wavelength) and half the amplitude of the previous octave.
Putting It All Together

This is an example of the six noise functions from earlier added together. In my project I have used 1D, 2D, and 3D noise, with anywhere from 4 to 12 octaves at a time. The lacunarity I rarely change, ranging to 1.95 to 2.05 in my project. I’ve used gains of 0.3 to 0.7. The low gain functions are geared toward large terrain features, whereas the highest gain functions are used to texture mountain ranges.